Оценка риска инвестиционных проектов

Риски различных инвестиционных проектов характеризуются вероятными значениями получения ожидаемых результатов. В связи с тем, что принятие решений происходит в условиях неопределенности, менеджеру требуется рассматривать несколько сценариев развития событий и, исходя из статистических данных за прошедший период, мнений экспертов или собственных прогнозов, выбрать наиболее приемлемый из них. По каждому из сценариев следует определить ожидаемый результат и оценить возможность его совершения.

Рассмотрим два инвестиционных проекта, по которым известна ожидаемая доходность и вероятность ее достижения (табл. 8.1).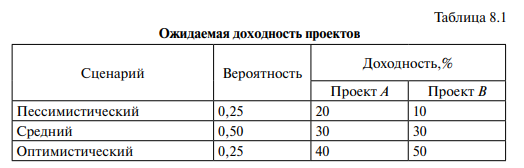

В таблице представлены данные по трем сценариям возможного развития событий: пессимистический, средний и оптимистический, а также вероятность их совершения. Сумма вероятностей равна единице.

Если на 1000 застрахованных было зафиксировано 25 несчастных случаев, то вероятность наступления этого события можно оценить как 2,5% (25 : 1000).

При прогнозировании сложных экономических ситуаций или при оценке новых инвестиционных проектов статистика о прошлом отсутствует. Поэтому менеджеры вынуждены прибегать к оценкам экспертов, финансовых консультантов, результатам научных исследований и к собственному опыту. В этом случае для получения объективного результата важен квалифицированный отбор экспертов и корректная обработка их мнений.

Имея экспертную оценку вероятности по каждому из сценариев, можно определить наиболее вероятный исход по каждому из проектов. Для этого рассчитывается ожидаемая доходность:

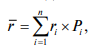
где r_i — доходность по сценарию i;

P_i — вероятность развития событий по сценарию i;
n — общее число возможных сценариев.

Исходя из возможных сценариев, для каждого из проектов наиболее вероятный результат составит: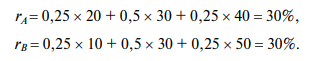

Мы видим, что наиболее вероятная доходность по проекту А и проекту В будет одинаковой и составит 30%. Однако вариация ожидаемых доходностей по проекту В больше и колеблется от 10 до 50%, в то время как по проекту А разброс доходностей ниже: от 20 до 40%. Уже на основе этих данных мы предварительно можем сказать, что проект В является более рискованным, так как отклонение ожидаемых доходностей от наиболее вероятного результата больше, что наглядно демонстрирует рис. 8.2.

Из рисунка видно, что при одинаковой средней доходности разброс доходностей по проекту В больше, чем по проекту А, что свидетельствует о большей степени риска проекта В. Для того чтобы оценить степень риска, необязательно строить графики показателей по проектам. Для этого применяются следующие измерители: дисперсия, среднеквадратическое отклонение, коэффициент вариации.

Дисперсия дискретного распределения рассчитывается по фор муле:

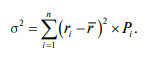
На основе представленных в табл. 8.1 данных определим дисперсию для проектов А и В:

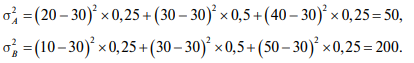
Таким образом, вариант В имеет более высокое значение дисперсии, и его можно оценить как более рискованный. Если менеджеры не склонны рисковать, то они отдадут предпочтение проекту А. На основе показателя дисперсии рассчитывают среднеквадратическое (стандартное) отклонение.

Стандартное отклонение рассчитывается по формуле:

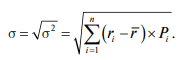
Стандартное отклонение измеряется в тех же единицах, что и оцениваемый показатель. Если мы пытаемся оценить доходность в процентах, то и стандартное отклонение также измеряется в процентах. В нашем примере стандартное отклонение для проекта А составит 50 = 7,07%, а для проекта В — 200= 14,1%, что подтверждает более высокий риск проекта В.

На основе показателей дисперсии и стандартного отклонения мы делаем вывод о большей рискованности проекта В. Данный вывод абсолютно справедлив, так как наиболее вероятная доходность по рассматриваемым проектам одинакова и составляет 30%. А как быть, если по одному проекту доходность и стандартное отклонение выше, чем по другому? Например, имеются следующие данные по проекту I и проекту II (табл. 8.2).

Исходя из данных, приведенных в таблице, можно сделать вывод, что проект I является более доходным по сравнению с проектом II, но одновременно он имеет и большую степень риска. Стандартное отклонение по первому проекту составляет 7,5%, а по проекту II только 6,1%. Для принятия решения в данном случае необходимо рассчитать коэффициент вариации (variation coefficient, CV).

Он рассчитывается как отношение стандартного отклонения к ожидаемому результату:

Чем выше коэффициент вариации, тем больше размер риска на единицу результата. Следовательно, проект I, имеющий более высокий коэффициент вариации, является более рискованным. Поэтому, несмотря на то что проект I имеет более высокую доходность, грамотный финансист предпочтет проект II, так как относительный риск (риск на единицу доходности) по данному проекту меньше.